【数学の考え方（全六回）】第一回　たし算・かけ算から学ぶ計算のしくみ　～アタリマエを疑う～

2020-05-122021-04-18

広大な世界へ…

このコーナーでは、少し難しく、興味深く、面白い内容を取り扱います。

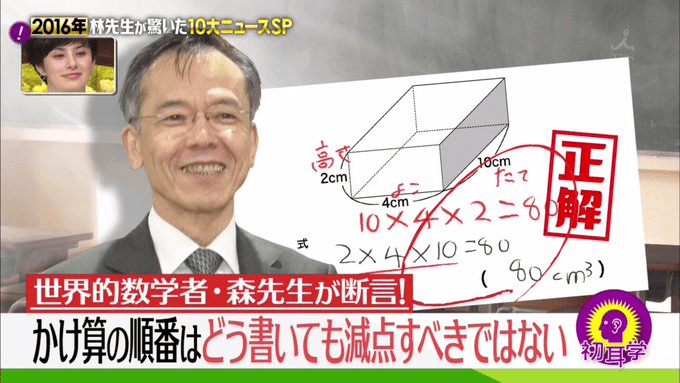
かけ算の順序問題

皆さんは「かけ算の順序問題」をご存じでしょうか？

Q.　リンゴが３個ずつ入った袋が全部で４袋あります。リンゴは全部でいくつありますか？

A1.　3×4＝12（個）

A2.　4×3＝12（個）

A1とA2はどちらも同じ答えを見ちびちだしていて、両方正解のように見えます。

しかし、小学校によってはA1の書き方のみを正解として、A2のような解答は認めない場合があったのです。

ここから、かけ算の順序問題が勃発しました。

具体的な内容は下記の動画やリンクを参照してください。

とある東大生はかけ算に順序が必要だと考えます｜Nao Harada｜note

かけ算の順序問題 – Wikipedia

上記のように、いろいろな意見があります。

一概にどちらが正しいとは言えませんが、私はこの問題については先ほどの問題と同様に「考える意味がない」と思っています。

それらは個人の定義や信条の問題で、人によって意見が変わってくるのは明々白々です。

皆さんはどう考えますか？

複素数の世界

私たちは先ほど、実数の世界まで旅をしてきました。

このような過程で、数の世界は様々に広がって行きます（自然数→整数→有理数→実数→・・・）。

しかし、ある意味での「数の世界の終着点」というものは存在します。

それは「複素数」と呼ばれる新たな数です。

複素数の定義

2乗すると -1 になる新しい数を1つ考えて、これを文字 $i$ で表し、虚数単位という（ $i^2 = -1$ ）。

2つの実数 $a,b$ を用いて $a + bi$ の形に表される数を複素数という。

複素数と言われると、素数と関係がありそうな響きですが、全く関係はありません。

2つの実数、つまり複数の要素から構成される数なので、日本語では「複素・数」と呼ばれています。

「複・素数」ではないので気を付けてください。（英語で複素数はcomplex number、素数はprime number）

なぜこの数が、ある意味での「数の世界の終着点」なのでしょうか？

それは、難しい言葉で答えるならば、

複素係数一変数多項式が複素数の根を持つ、つまり、代数的に閉じているから。

となります。

わかりやすく噛み砕いて説明すると、

数学には「代数学の基本定理」という、方程式の解に関する非常に重要な定理があります。この定理の要点は

n次方程式には（複素数の範囲で）必ずn個だけ解が存在する。

です。

つまり、代数学の主要な考察対象である「多項式」について、その根（＝方程式の解）は、必ず複素数の世界の中にあるということを意味します。

ここで、先ほど紹介した言葉「閉じている」のイメージから連想させると、

複素数の世界は「代数的に閉じている（＝多項式の根は必ず複素数である）」

と表現できます。

上記の説明をもっともっと単純に説明すると、

複素数さえあれば、 $x^5 + x^3 + 1=0$ などの $x$ に関するn次方程式の解がすべて表現できる。

⇒　高度な数学を習わない高校までは、複素数さえあれば十分じゃない？

というイメージです。

群・環・体について

先ほどまでは、ある計算がある世界で閉じていることが重要だと述べました。

この考え方は、現代数学の源泉である「群・環・体」の理論へとつながっています。

この理論を一言で説明すると、

「代数学のエッセンスを抽出して一般化した、幅広い分野の基礎として役立つもの」

です。

以下、計算→演算、世界→集合と言い換え、演算の正確な定義と群環体それぞれの定義を述べます。

定義が難しく感じる方はそこを読み飛ばして、群環体の具体例だけでも確認してみてください。

抽象的な物事を学ぶ際は、具体例を確認することが上達への最短ルートですよ！

演算の正確な定義

$X$ が集合であるとき、写像 $\phi : X \spadesuit X \to X$ のことを集合 $X$ 上の演算という。混乱の恐れがない時には、 $\phi(a,b)$ の代わりに $ab$ と書く。

群の定義

$G$ を空集合ではない集合とする。 $G$ 上の演算が定義されていて次の性質を満たすとき、 $G$ を群という。

単位元と呼ばれる元 $e \in G$ があり、すべての $a \in G$ に対し $ae = ea = a$ となる。
すべての $a \in G$ に対し $b \in G$ が存在し、 $ab = ba = e$ となる。この元 $b$ は $a$ の逆元とよばれ、 $a^{-1}$ と書く。
(結合法則)　すべての $a,b,c \in G$ に対し、 $(ab)c = a(bc)$ が成り立つ。

群の具体例

$G =$ 整数、有理数、自然数の集合は通常の加法+により可換群（交換法則が成り立つ）

$G =$ （0を除いた）有理数、実数の集合は通常の乗法×について可換群

環の定義

集合 $A$ に二つの演算 $\heartsuit$ と $\spadesuit$ (加法・乗法、あるいは和・積)が定義されていて、次の性質を満たすとき、 $A$ を環という。以下、 $a \spadesuit b$ の代わりに $ab$ と書く。

$A$ は $\heartsuit$ に関して可換群になる。
(積の結合法則) 　すべての $a,b,c \in A$ に対し、 $(ab)c = a(bc)$ 。
(分配法則)　すべての $a,b,c \in A$ に対し、 $a(b \heartsuit c) = ab \heartsuit ac$ 、 $(a \heartsuit b)c = ac \heartsuit bc$
乗法についての単位元 $1$ がある。つまり、 $1a = a1 = a$ がすべての $a \in A$ に対して成り立つ。